Direct Multichannel Tracking

Carlos Jaramillo, Yuichi Taguchi, Chen Feng

May 2017

PDF Poster Video DOI Supplementary Materials

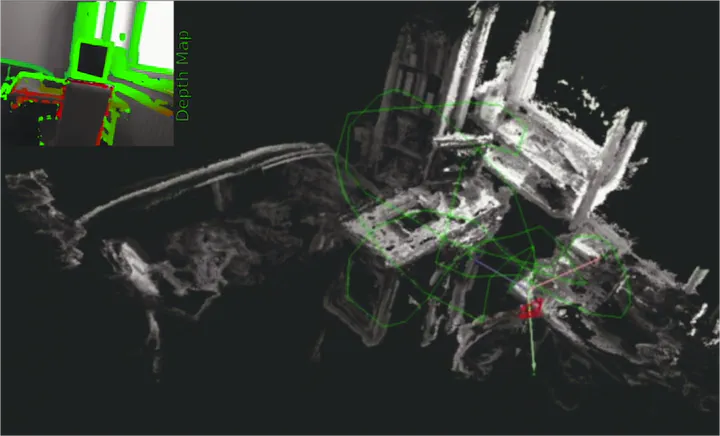Depth map and 3D reconstruction of Room sequence from the LSD dataset

Abstract

We present direct multichannel tracking, an algorithm for tracking the pose of a monocular camera (visual odometry) using high-dimensional features in a direct image alignment framework. Instead of using a single grayscale channel and assuming intensity constancy as in existing approaches, we extract multichannel features at each pixel from each image and assume feature constancy among consecutive images. High-dimensional features are more discriminative and robust to noise and image variations than intensities, enabling more accurate camera tracking. We demonstrate our claim using conventional hand-crafted features such as SIFT as well as more recent features extracted from convolutional neural networks (CNNs) such as Siamese and AlexNet networks. We evaluate the performance of our algorithm against the baseline case (single-channel tracking) using several public datasets, where the AlexNet feature provides the best pose estimation results.

Type

Conference paper

Publication

In 3D Vision (3DV), International Conference on, IEEE.

Theory

The following figure explains the pipeline of the DMT system:

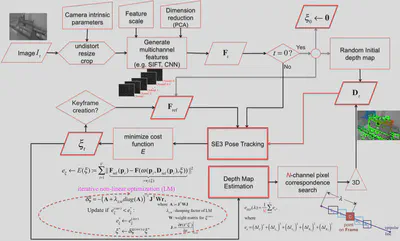
DMT System Pipeline

The single channel energy equation for photometric alignment is $$ E(\xi ) = \sum\limits_{i = 1}^V {{{({{I_K}({{\bf{p}}_i}) - I(\omega ({{\bf{p}}_i},{{\bf{D}}_K}({{\bf{p}}_i}),\xi ))})}^2}} $$

where ${\bf \xi}$ is a $6$-vector representing the pose of the current image $I$ with respect to the reference image $I_K$ in Lie algebra $\mathfrak{se}(3)$, and $\omega$ is the 3D projective warp function that maps the pixel location ${\bf{p}}_i$ in the reference image according to its inverse depth $D_K ({\bf{p}}_i)$ and the pose ${\bf{\xi}}$ to the pixel location in the current image.